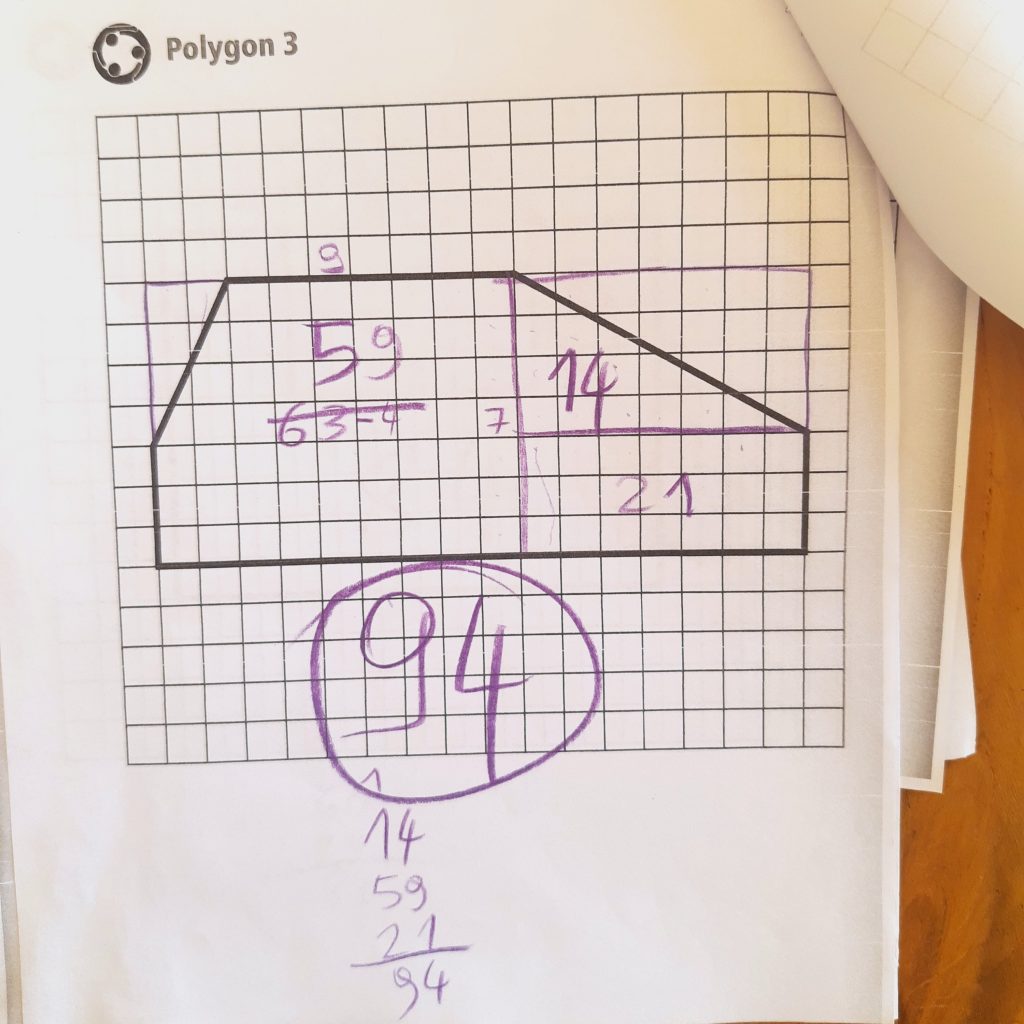
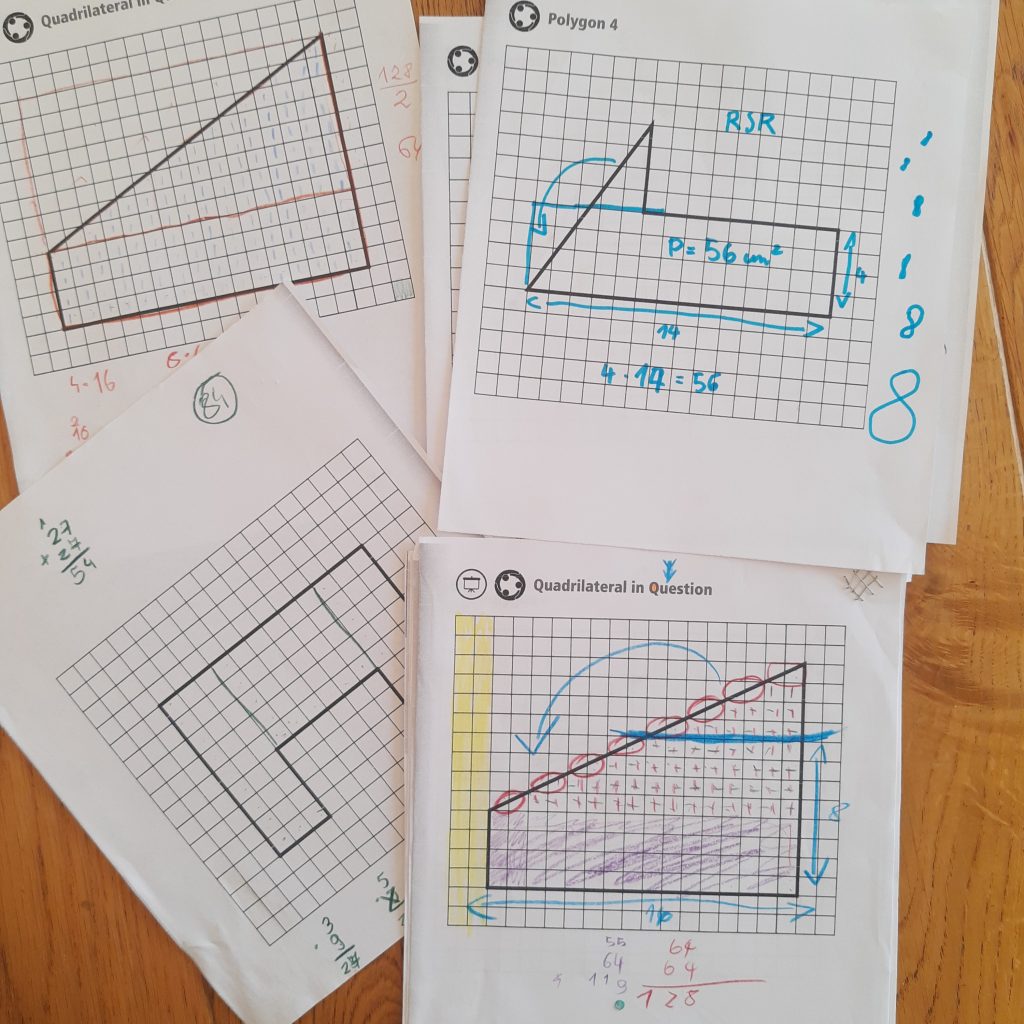
Podczas naszych zajęć matematycznych we wrześniu zajęliśmy się ulubioną dziedziną matematyki – geometrią. Zaczęliśmy od sprytnego obliczania pola wielokątów przez poszukiwanie w nich trójkątów prostokątnych i liczenie ich powierzchni jako połowy prostokąta, który mogą utworzyć. Dla mnie uważne spojrzenie i doszukiwanie się regularności w figurach jest ważniejsze niż znajomość wzorów na pola figur, bez zrozumienia skąd się te wzory wzięły.
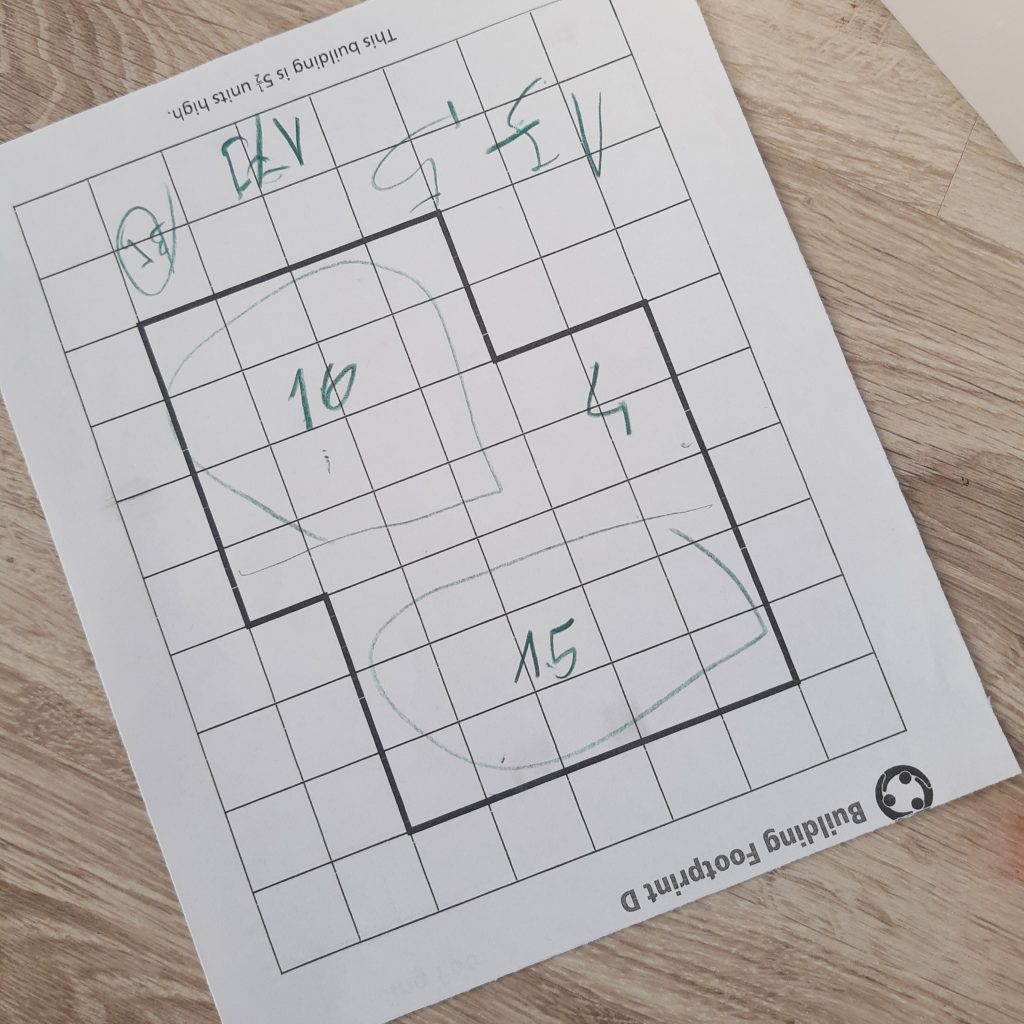
Potem z tych naszych figur płaskich stworzyliśmy piętrowe biurowce (namacalnie, z kostek, jeśli ktoś potrzebował), mnożyliśmy pole figur przez ilość pięter, uzyskując w ten sposób objętość. Dla utrudnienia pięter było 5 i pół ale i z tym większość sobie poradziła, z pomocą klocków lub bez.
No i skoro było tyle szukania trójkątów prostokątnych to za naturalne uznałam, że pora przedstawić grupie kolejnego (po Archimedesie, Erastotenesie, Fibonaccim i Leibnitzu) znanego matematyka, Pitagorasa. A był to przecież nie byle kto, całkiem barwna postać, znana większości z nas tylko z twierdzenia, którego prawdopodobnie akurat nie wymyślił. Wiemy że Pitagoras:
- był Grekiem i żył ok. 500 r. p.n.e.
- uważał, że wszystkie zawiłości wszechświata da się opisać przy pomocy matematyki
- odkrył, że wysokość dźwięku drgającej struny zależy od jej długości – jeśli strunę skróci się o połowę to dźwięk podnosi się o oktawę
- liczba 10 była dla niego liczbą boską, bo była to suma czterech pierwszych liczb, oznaczających cztery żywioły (1+2+3+4=10)
- założył stowarzyszenie miłośników nauki (i jego samego), uznawane przez wielu za sektę, w którym przez pierwsze 5 lat Pitagorasa można było oglądać jedynie zza kurtyny
- członkowie jego związku musieli przestrzegać wielu dziwnych zasad, jak zakaz sikania w stronę słońca czy zakaz jedzenia bobu i każdy z tych zakazów miał logiczne wytłumaczenie
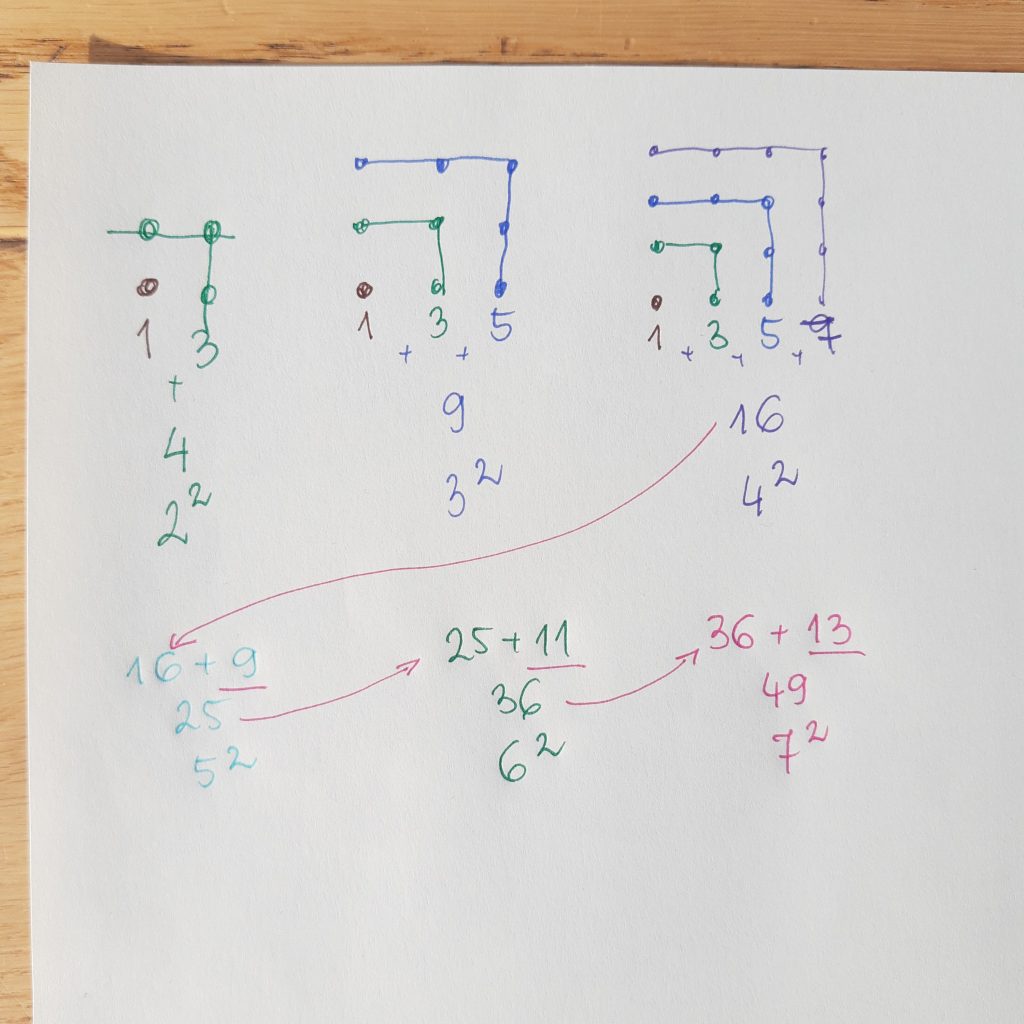
Pitagoras odkrył też ciekawą regułę dotyczącą kwadratów (a te przecież wiążą się z jego słynnym twierdzeniem) – mianowicie, że suma kolejnych liczb nieparzystych daje kwadraty kolejnych liczb, czyli 1+3=4 czyli 2², 1+3+5=9 czyli 3², 1+3+5+7=16 czyli 4² itd. Te kwadraty dobrze widać gdy się je ułoży z kamyków, czy jak u nas ze szklanych kulek.
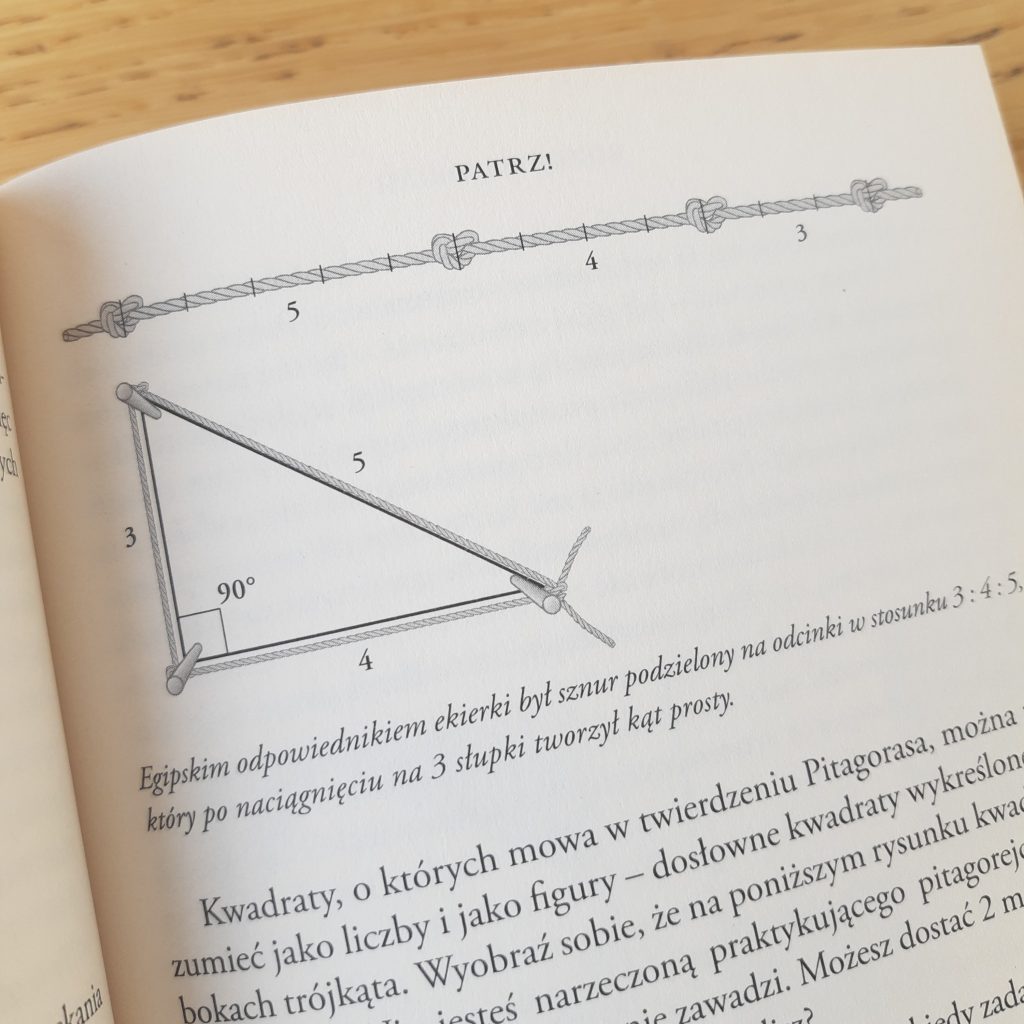
Ale po resztę twierdzenia to już prawdopodobnie Pitagoras wybrał się do Egiptu. Tam spotkał się z magicznym sznurkiem konstruktorskim, którego Egipcjanie używali do wyznaczania kątów prostych na budowach. Sznurek ten składał się z odcinków o długości 3, 4 i 5 miar. Ta trójka jest obecnie zwana trójką egipską – 3 odcinki o tej długości tworzą trójkąt prostokątny. Znane nam twierdzenie powinno się więc raczej nazywać twierdzeniem egipskim ale cóż. My sobie ten sznurek odtworzyliśmy, żeby to sprawdzić ale ledwo nam się zmieścił w pracowni 🙂 Ale kąt prosty wyszedł idealny (porównaliśmy do brzegu dywanu).
Używając tabliczki twierdzenia Pitagorasa od Edudomo poprosiłam młodzież aby napisali czy gdyby nasze kwadraty były ze złota to czy wybraliby jeden duży czy dwa małe. Odpowiedzi podzieliły się równo, pół na pół (ciekawe, że wszystkie dziewczyny wybrały zgodnie dwa małe). Potem wypełnili powierzchnię kwadracikami i przekonali się, że nikt by na swoim wyborze nie zyskał.
Koncepcja budowy trójkątów i równości pomiędzy ich polami jeszcze była do ogarnięcia ale późniejsze obliczenia z wyciąganiem pierwiastka z pola dużego trójkąta wymagało już dużo wsparcia (pomimo rozumienia pierwiastków). To jednak podstawa programowa z 8 klasy a nasza grupa to głównie klasy 5-6. Ale z lekkim wsparciem policzyliśmy obwody naszych wielokątów z poprzednich ćwiczeń. Tutaj też na razie nie dochodziliśmy do wzoru na twierdzenie Pitagorasa, skupiliśmy się praktyce. Moim zdaniem nauka na pamięć wzorów (czy tabliczki mnożenia) nie ma sensu dopóki się ich dogłębnie nie doświadczy i nie zrozumie. A wtedy często już nie trzeba się ich uczyć.
Spojrzeliśmy też na kilka dowodów na twierdzenie Pitagorasa, a jest ich wiele, niektóre podobno pochodzą sprzed czasów Pitagorasa, ze starożytnych Chin. Opublikowano podobno około 120 dowodów geometrycznych na to twierdzenie, jeden z nich należy nawet do Leonardo da Vinci a inny do amerykańskiego prezydenta Jamesa Garfielda.
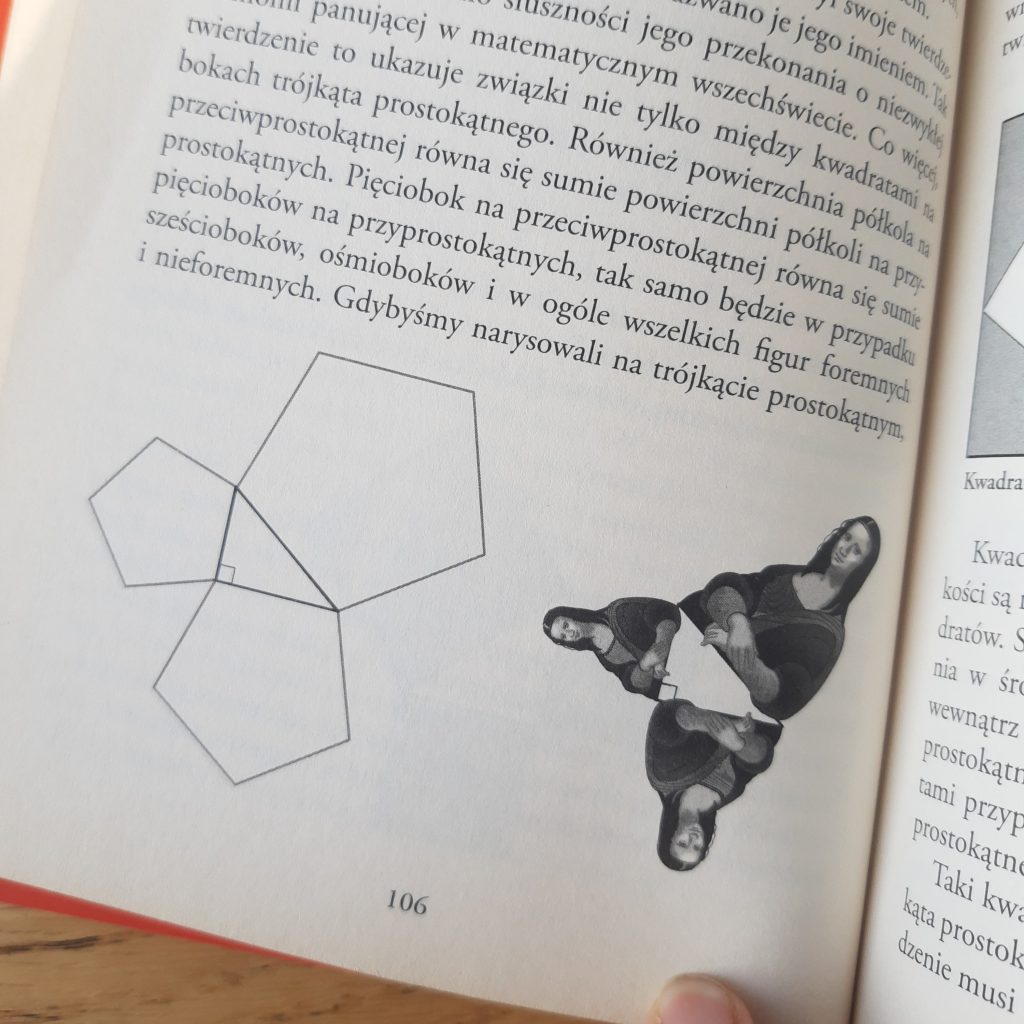
I jeszcze jedna ciekawostka – nie tylko między trójkątami zbudowanymi na bokach trójkąta prostokątnego zachodzi znana nam zależność pitagorejska- tak samo będzie z każdą figurą utrzymującą proporcje – ta zbudowana na przeciwprostokątnej będzie miała takie samo pole jak obie zbudowane na przyprostokątnych razem wzięte (patrz przykład z Mona Lisą).
Ciekawostki o Pitagorasie na podstawie książki „Przygody Alexa w krainie liczb” Alexa Bellosa.